|
|||||
|
|
|||||
| 画多边形 | |||||
| 多边形基本概念 | |||||
| 美丽的镶嵌 | |||||
| 多边形的应用 | |||||
|
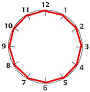
1.利用右方时钟以及直尺来完成以下绘图。在数的时候要小心。 |
|
a.从1点钟开始,每次加上2小时直到你回到1点钟的位置。 请问在时钟内你得到了哪一种多边形呢? 答:形成的六边形,如下图。 |
|
如同a.小题,每次加上4小时。 你会得到何种多边形呢? 答:形成一个三角形,如图。 |
|
|
|
如果你每次加上1小时,会得到何种多边形呢? 答:形成的十二边形,如下图。 |
|
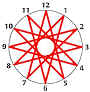
从1点钟开始,每次加上5小时,持续步骤直到你回到1点钟的位置。完成这个动作,你会得到一个星形。这个星形有几的顶点呢? 答:此星形有12的顶点,如下图。 |
|
|
|
再次观察每加上3小时得到的多边形: a. 如果你从1点钟、2点钟、……、12点钟出发,在时钟里你可以得到几个不同位置的此种多边形呢? b. 在时钟内,将a.小题中得到所有不同位置的此种多边形,用不同颜色表示出来。 答:此多边形在时钟内有三种位置。你可以从一点钟、两点钟,或三 点钟出发。 如果你从四点钟出发,得到的正 方形会和从一点钟出发的相同。 依此类推,将会得到三种不同位 置的正方形。 |
|
|||
|
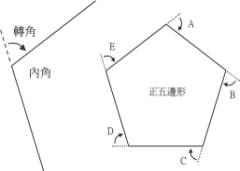
2.a. 如果你沿着一个正五边形的边,经过A、B、C、D、E五个转角走了一圈,你共转了多少度呢?如果改成绕正方形或正三角形,你又转了多少度呢?b. 如果你沿着任意多边形的边走一圈,你总共转了多少度?为什么?对于所有的多边形所转的角度有着什么样的关系呢? |
|
|||
|
答:a. 对于每种情形,无论是正五边形、正方形或正三角形,你都转了360度。
b.
若你沿着任意多边形走,你将转了360度。 若在你开始正要走时,你的脸朝着某一方向。当你走并且转完最后一个弯之后,你的脸会朝着一开始的那个方向。所以你转个一个圈,就是360度。 |
||||
|
a. 当你沿着正五边形走,你会转五个弯。请问每个弯所转的角度是多少? b. 正五边形的每个内角是几度呢? c. 你如何利用每个弯所转的角度,来求得任意正多边形的内角角度呢? |
b.
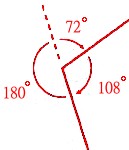
108度。一个平角(180度)减掉每个弯所转的角度(72度)等于108度。
有些学生会由画出这个角来得到这个关系: c. 将360度除以转角的个数。得到的答案就是每个转角的度数。然后再用180度减去每个转角的度数,就能得到此正多边形内角的角度。 |
|||
|
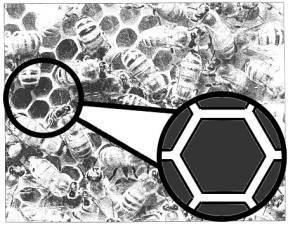
这是张蜜蜂与蜂巢的照片。
|
3.a. 你在图片中看到何种多边形?
b.
你所找出的多边形,它的每个内角各为多少度?
答:a.
由照片可看到六边形。 b.
此正多边形的每个内角量出来是120度。参考方法如下:
|
|||